Sound and Symmetry
Did you know that musical harmony mirrors symmetry in physical objects ? If you want to understand how this works, watch the following video and then keep scrolling...
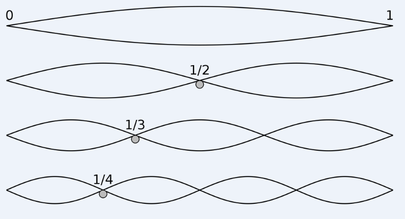
In the above video, each harmonic of a single fundamental frequency produces a regular polygon with the same amount of sides as that harmonics number. What you are seeing here are circular harmonics, just like a vibrating guitar string only circular.
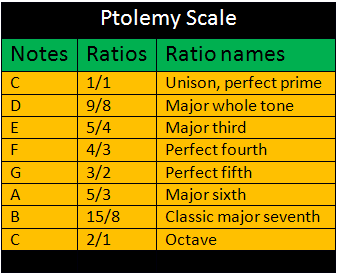
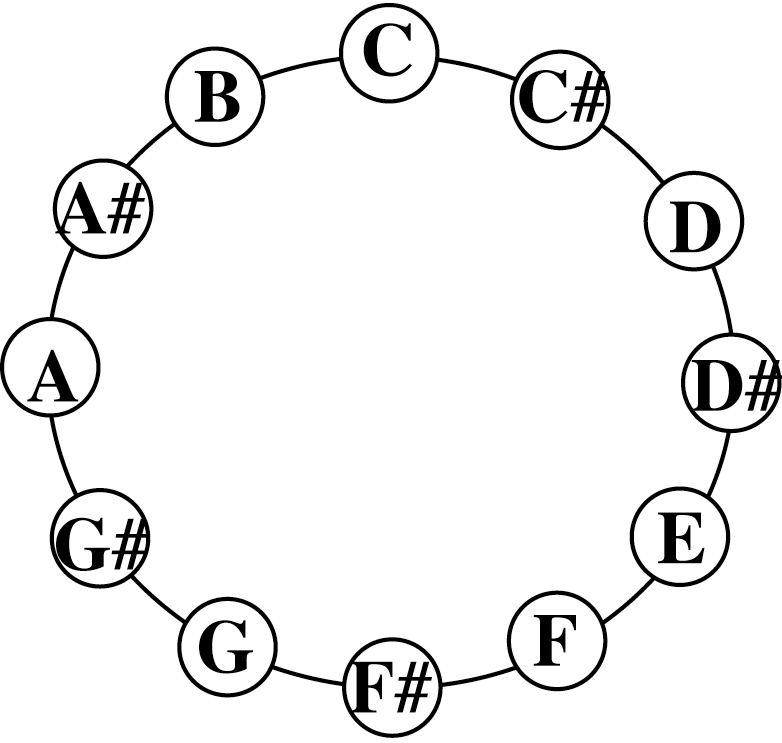
All of the ratio based intervals that we use in music are found in the spaces between these harmonics. The ratio for each interval tells you which two harmonics that interval is found between. The modern day diatonic music scale is based on this ratio based scale and sounds just about the same, so both have the same source.
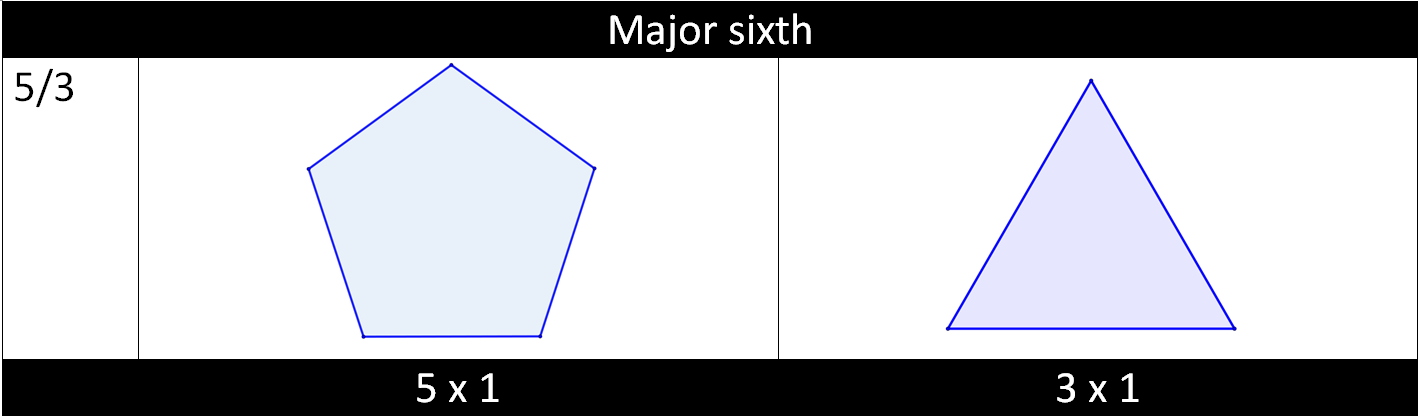
With this in mind, it makes some kind of sense to visualize musical intervals as combinations of regular polygons.
This might seem like an interesting but also fairly pointless thing to do. Regular polygons are defined as shapes that evenly divide a circle in 2D, but no polygon really has different properties to the others. When you move up one dimension and use regular polygons to evenly divide a sphere in 3D however, then some very interesting things are revealed.
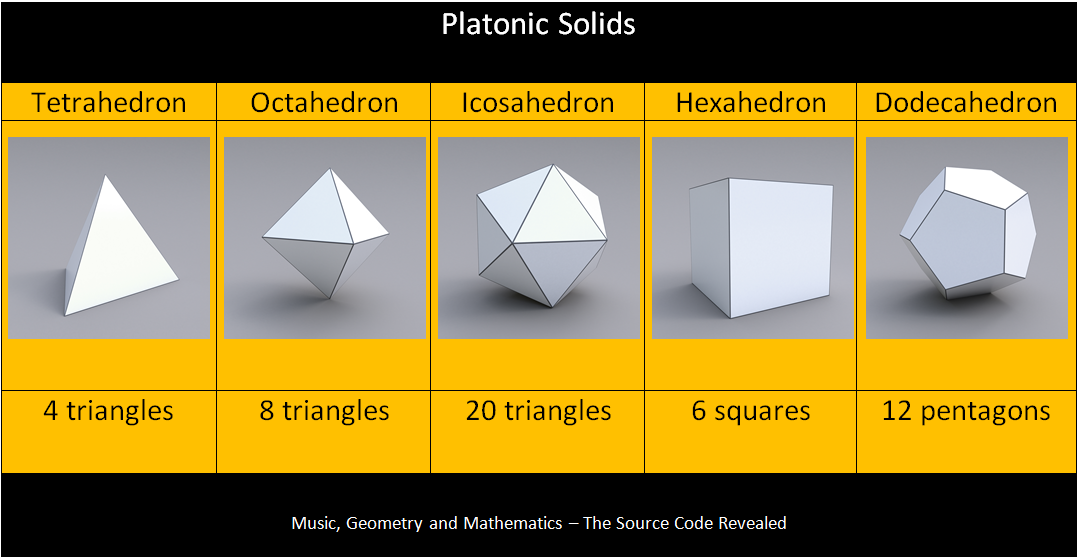
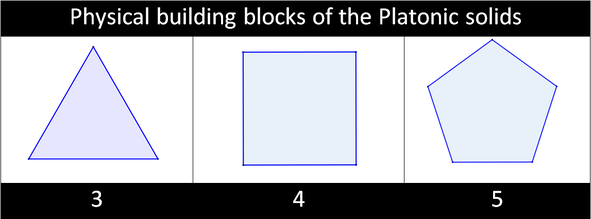
There are actually only 5 different ways to divide a sphere exactly evenly, the 5 unique shapes you get when you do this are called the Platonic solids. A Platonic solid is a regular, convex polyhedron. They are made from identical-in-shape-and-size, regular polygonal faces with the same number of faces meeting at each vertex. All corners must also touch the outside of a sphere, dividing it into even parts. Basically, every side and angle in each shape is exactly the same, making them perfectly uniform. These are the simplest and most uniform 3 dimensional shapes that exist, and for this reason they have been studied, loved and used in the construction of our world for thousands of years.
There are actually only 5 different ways to divide a sphere exactly evenly, the 5 unique shapes you get when you do this are called the Platonic solids. A Platonic solid is a regular, convex polyhedron. They are made from identical-in-shape-and-size, regular polygonal faces with the same number of faces meeting at each vertex. All corners must also touch the outside of a sphere, dividing it into even parts. Basically, every side and angle in each shape is exactly the same, making them perfectly uniform. These are the simplest and most uniform 3 dimensional shapes that exist, and for this reason they have been studied, loved and used in the construction of our world for thousands of years.
Notice how the Platonic solids are made from only triangles, squares and pentagons.
If we look back at the levitated drop of water video, 3, 4 and 5 sided polygons make a 3-4-5 major chord. This chord can be played in any key, for example 300 Hz, 400 Hz and 500 Hz. In the following video higher octaves of 3, 4 and 5 Hz were used.
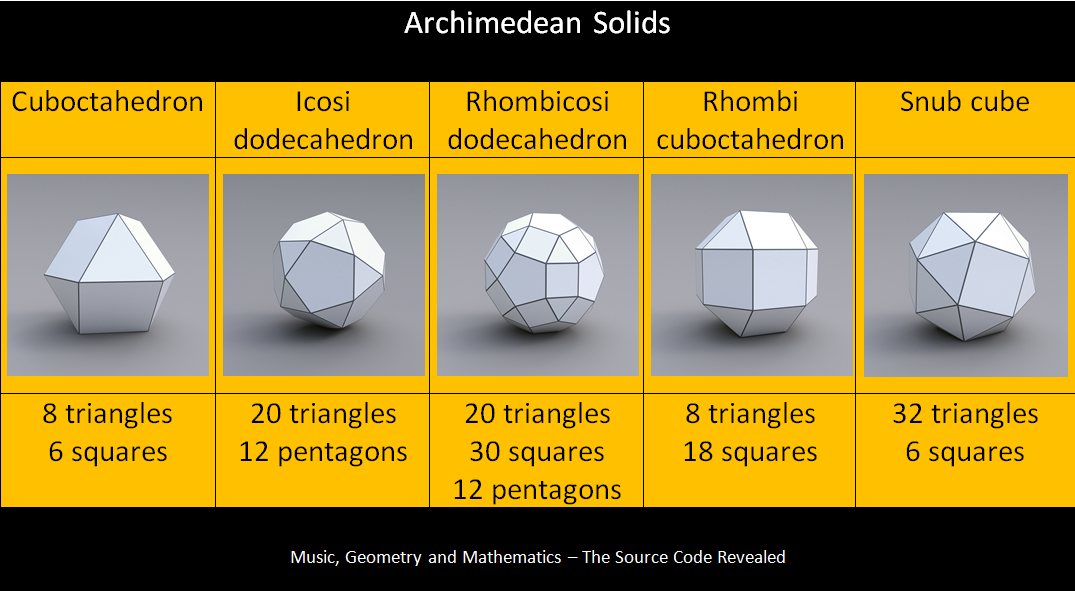
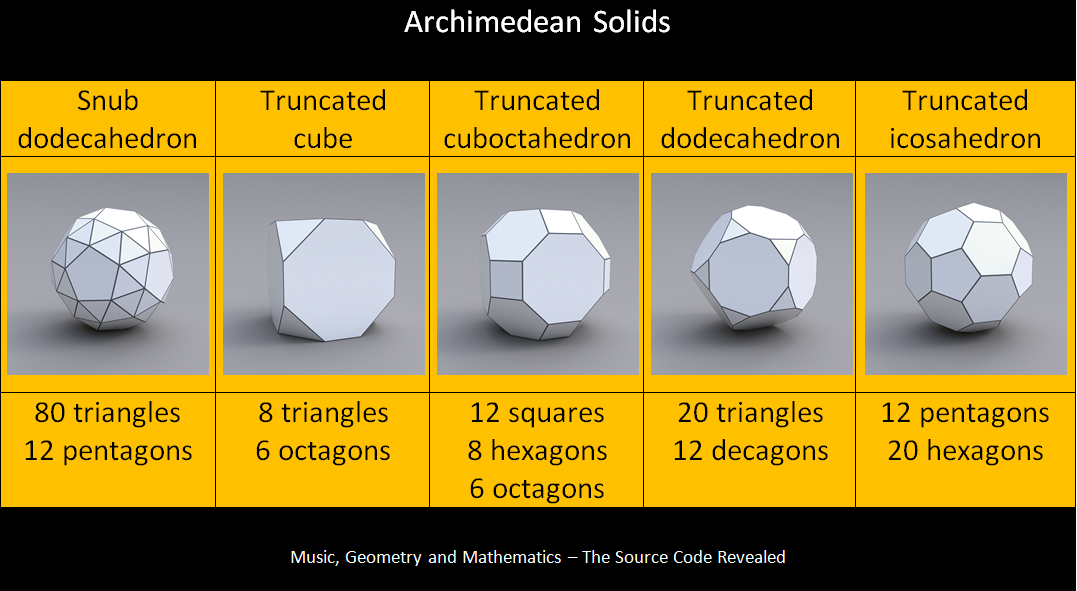
If you use more than one type of regular polygon together in one shape, you can make the Archimedean solids. Obviously these are named after Archimedes and only 13 of them exist. The Archimedean solids are referred to as the semi-regular polyhedra, because they are not 100% regular like the platonic solids are. Although they are not 100% regular, all of the edges in these are also exactly the same length making them the next most regular shapes after the Platonic solids. Many interesting things including soccer balls and geodesic domes are made from these.
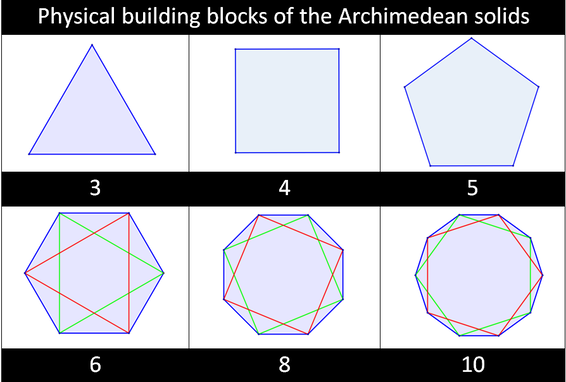
As with the Platonic solids, these are made from triangles, squares and pentagons, but they also contain hexagons, octagons and decagons. The hexagon however can be made from 2 triangles, the octagon from 2 squares, and the decagon from 2 pentagons. So the Archimedean solids can also be made from only triangles, squares and pentagons.
In the following video you can hear the 3 - 4 - 5 - 6 - 8 - 10 major chord. This is the same 3 - 4 - 5 major chord that the Platonic solids make, only with another of the same chord an octave above it. Each octave pair represents two polygons with half / double the amount of sides as each other.
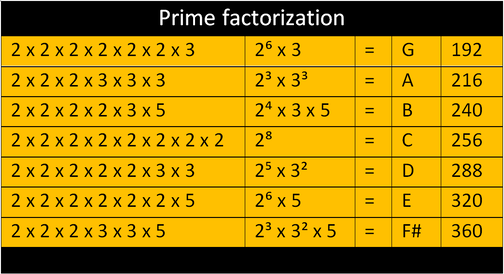
If you look back at the images of the Archimedean and Platonic solids, you will see that the amount of sides in each polygon, and also the amount of polygons in each solid are always 5-smooth numbers. These are numbers that don't have any prime factors larger than 5. In this image you can see how some larger 5-smooth numbers are made by multiplying the prime numbers 2, 3 and 5 together in various ways. You cannot use a larger prime number like 7, 11 or 13 to make these numbers.
2, 3 and 5 alone make an inverted major chord, from this chord you can shift the notes by octaves (x2) to make any other inversion of the major chord. You can actually make a whole music scale with 2, 3 and 5, for example the ratio based scale at the start of this page has only 5-smooth numbers in its ratios. The image above is actually the same scale, only it starts in G instead of C and shows Hz frequencies and not ratios. In the following video you can hear 2, 3 and 5 as a major chord.
You cannot make any symmetrical solids with polygons that have 7, 11 or 13 sides (prime numbers larger than 5). Polygons with these amounts of sides just don't fit together.
For some reason it is also impossible to make a perfectly symmetrical solid using a prime number larger than 5 as the amount of sides. Heptahedrons with 7 sides for example are not very uniform and can never divide a sphere evenly. The situation gets even worse with higher prime numbers.
Musical ratios containing prime numbers larger than 5 tend to sound quite odd, which is why no similar sounding intervals are found in the normal 12 tone equal temperament scale. That is not to say they are all bad, they just represent tension more. Below you can hear a 7-limit, an 11-limit and a 13 limit interval.
Here are some 5-limit intervals, these have only got 5-smooth numbers in their ratios and sound a lot more pleasing to the ear: Octave = 1/2, Perfect fifth = 3/2, Major third = 5/4.
So it seems like a direct connection between good sounding intervals and symmetrical geometry does indeed exist. Prime numbers up to 5 make good sounding musical intervals and strong symmetrical 3D shapes, while larger primes makes strange sounding intervals and can't make strong symmetrical 3D shapes. Here are some images of interesting that have 5-smooth numbers at their core.
Here is some music that was made using 5-limit tuning, this tuning works very well for calming your mind:
The reason why 5-smooth numbers work better in physical objects is easy to see. Higher prime numbers just won't fit together in a symmetrical way.
Musical intervals with regular numbers in their ratios (i.e., ratios involving small prime integers like 2, 3, and 5) tend to sound more consonant, pleasing or "better" to the human ear because their frequencies have simpler mathematical relationships. This simplicity allows our brains to easily process and recognize patterns, creating a harmonic sensation.
When the ratios of two frequencies involve prime numbers no higher than 5, there are more common overtones or harmonics between the sounds. This simplicity allows our brains to easily process and recognize patterns, creating a harmonic sensation.
When the ratios of two frequencies involve prime numbers higher than 5, there are fewer common overtones or harmonics between the sounds. The resulting complexity in the relationship between the frequencies makes it harder for our auditory system to process and form recognizable patterns, leading to a more dissonant or rough sensation.
If you find all of this to be interesting, the story does not end here. The Babylonians, Maya and various other ancient cultures had a strong preference for 5-smooth numbers. You can learn more about this on the next page.
Musical intervals with regular numbers in their ratios (i.e., ratios involving small prime integers like 2, 3, and 5) tend to sound more consonant, pleasing or "better" to the human ear because their frequencies have simpler mathematical relationships. This simplicity allows our brains to easily process and recognize patterns, creating a harmonic sensation.
When the ratios of two frequencies involve prime numbers no higher than 5, there are more common overtones or harmonics between the sounds. This simplicity allows our brains to easily process and recognize patterns, creating a harmonic sensation.
When the ratios of two frequencies involve prime numbers higher than 5, there are fewer common overtones or harmonics between the sounds. The resulting complexity in the relationship between the frequencies makes it harder for our auditory system to process and form recognizable patterns, leading to a more dissonant or rough sensation.
If you find all of this to be interesting, the story does not end here. The Babylonians, Maya and various other ancient cultures had a strong preference for 5-smooth numbers. You can learn more about this on the next page.