Harmonic Series
When things vibrate harmonics usually appear, so the laws of harmonics are really the most fundamental laws that govern all of vibration. Since almost everything vibrates on some level, understanding the harmonic series is a good way to learn something about almost anything in the universe. Music and sound are the easiest medium to use for learning about harmonics, this is because these vibrations are within human hearing range and are therefore very easy to perceive.
The simplest way to express the harmonic series is with all of the whole numbers starting from 1. For example 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18... This could also be 100, 200, 300, 400, 500... Or even 108, 216, 324, 432, 540... To generate the harmonic series for any number just add it to itself (exactly like starting the Fibonacci series), then add it to your answer each time instead of adding the last number in the series as you do with the Fibonacci series. So for 100 you would add 100 making 200, then add another 100 making 300, then another hundred making 400 and so on.
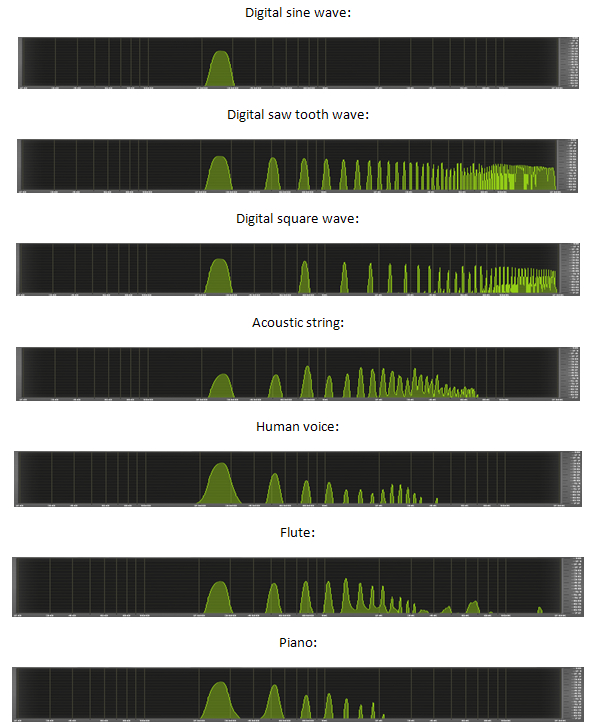
Below are some spectrum analyzer images of the note C played with various commonly used musical sounds. The tone on the far left is the main fundamental frequency of C while the higher tones to the right are its harmonic overtones. If the first harmonic (on the far left of each image) was 100 Hz, then the second one would be 200 Hz, the third 300 Hz and so on. They always follow the same 1, 2, 3, 4, 5, 6, 7, 8, 9... whole number pattern no matter what number you start with.
You can see that the intervals between the harmonics are the same but that the volumes are different, it is these variations in the volume of each overtone that make each instrument sound unique. If you play a higher or lower note on the same instrument then the whole structure simply moves to the left or right (on the spectrum analyzer). This is because the intervals between the harmonics are fixed and never change in relation to the fundamental frequency. The fundamental frequency and all of the overtones are a type of sound called a sine wave, this is the only type of sound that has no overtones of it's own.
The simplest way to express the harmonic series is with all of the whole numbers starting from 1. For example 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18... This could also be 100, 200, 300, 400, 500... Or even 108, 216, 324, 432, 540... To generate the harmonic series for any number just add it to itself (exactly like starting the Fibonacci series), then add it to your answer each time instead of adding the last number in the series as you do with the Fibonacci series. So for 100 you would add 100 making 200, then add another 100 making 300, then another hundred making 400 and so on.
Below are some spectrum analyzer images of the note C played with various commonly used musical sounds. The tone on the far left is the main fundamental frequency of C while the higher tones to the right are its harmonic overtones. If the first harmonic (on the far left of each image) was 100 Hz, then the second one would be 200 Hz, the third 300 Hz and so on. They always follow the same 1, 2, 3, 4, 5, 6, 7, 8, 9... whole number pattern no matter what number you start with.
You can see that the intervals between the harmonics are the same but that the volumes are different, it is these variations in the volume of each overtone that make each instrument sound unique. If you play a higher or lower note on the same instrument then the whole structure simply moves to the left or right (on the spectrum analyzer). This is because the intervals between the harmonics are fixed and never change in relation to the fundamental frequency. The fundamental frequency and all of the overtones are a type of sound called a sine wave, this is the only type of sound that has no overtones of it's own.
Without these intervals the sound will just be a noise, for it to be a musical tone it needs to have this exact arrangement of overtones that you see mirrored in all of the sounds above. Some sounds like certain stringed instruments can distort the harmonic series slightly making the intervals a bit too big, while other sounds like bells and gamelans have there own strange and completely unique overtones not in this "classic" overtone series. Generally however, musical sounds will usually have this harmonic arrangement.
With digital sound synthesis you can arrange computer generated sine waves according to the harmonic series to create sounds, the next video shows you how the classic synthesizer wave forms are made in this way:
If you look at the numbers at about 0:50 in the following video, you will see that the "Zipf's law" and the harmonic series are really one and the same. If you look near the end of the "overtones, harmonics and additive synthesis" video above, you will see that the sawtooth waves harmonics follow this law not only in frequency as all sounds do, but also in amplitude.
Anything that oscillates or vibrates has a fundamental frequency and harmonic overtones. Sound, light, atoms, orbits, electric currents and rotating machines are all vibrations which is why you find these same harmonics intervals playing important roles in many seemingly unrelated fields.
Quantum physics is all about waves, and everything is made from quantum stuff.
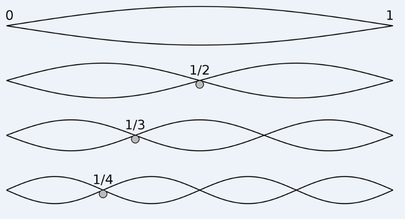
The following video explains how bridges collapse due to harmonic resonance. In it you can clearly see the bridge wobbling at 1/2 or one octave of the length of the middle part of the bridge.
The following video explains how harmonics apply to electricity. This video is quite long and boring, but you can skip to 7 minutes to see just the important part if you are really interested in this:
As I mentioned before, sound is the best way to experience and so truly understand how harmonics work. This is because sound is vibration that is within the human hearing range, and so it can be perceived and experienced directly. The sounds of a mono-chords and overtone chanting are some of the best places to hear harmonics, both of these sound generation methods amplify the harmonics of the fundamental pitch one at a time so that you can hear them as a very familiar melody.
Here is a video with mono-chord and overtone chanting at the same time: (this man is a master of overtones)
Here is a video with mono-chord and overtone chanting at the same time: (this man is a master of overtones)
Cymatics and geometry
When you see a cymatics video of a metal plate with sand or water being vibrated with sound, you will see that amazing patterns are made by certain frequencies. If the frequency is swept upwards, the patterns will jump out at certain points. These get more complex with higher frequencies and simpler with lower ones.
It is important to remember that the patterns do not happen with certain frequencies because they are special, they happen because those frequencies are the same as the root pitch and harmonics of the plate or drop of water itself. They are really dividing the plate into equal portions with the sand collecting in the parts that are not vibrating. If you were to use a violin bow on it from various angles, you would be able to make it ring these same tones. This would be easier than searching for them by sweeping a sine wave around.
So to really understand cymatics you need to remove the vibrating plate, as its size and shape influence the patterns in the sand or water too much. The short video below called “Shape oscillation of a levitated drop in an acoustic field” is the purest form of cymatics I have seen. In this video they have taken a transducer and aimed it at a reflector so that the sound bounces back at it. This creates a standing wave with pockets of high and low air pressure that are fixed in place and don’t move at all. When this happens you can place small objects or drops of water in these pockets and they will float in the air! This is good for cymatics, as now you only need to worry about the resonant frequency of the water drop itself, and not its container as well.
In the video they play the fundamental frequency of the drop of water, and it flattens into a disk. Then they modulate it at the first harmonic (octave) of this pitch and it becomes elongated, like a sausage. This sausage, however, is oscillating. The ends move together and the sides move apart, forming new ends so that it was like a “plus symbol” but with only one line visible at a time, at the peak of each oscillation. When they modulate the frequency at the third harmonic the water forms a triangle, also oscillating with another one so that both together would be a Star of David, but only one was fully formed at a time.
And so they go on. Each harmonic’s shape has the same amount of sides as its sequence number; 1 = circle, 2 = sausage, 3 = triangle, 4 = square, 5 = pentagon and so on. Obviously cymatics made using metal plates and other objects are just showing you complex versions of these basic shapes, made so by the extra factors being brought in by the objects’ physical properties.
So to really understand cymatics you need to remove the vibrating plate, as its size and shape influence the patterns in the sand or water too much. The short video below called “Shape oscillation of a levitated drop in an acoustic field” is the purest form of cymatics I have seen. In this video they have taken a transducer and aimed it at a reflector so that the sound bounces back at it. This creates a standing wave with pockets of high and low air pressure that are fixed in place and don’t move at all. When this happens you can place small objects or drops of water in these pockets and they will float in the air! This is good for cymatics, as now you only need to worry about the resonant frequency of the water drop itself, and not its container as well.
In the video they play the fundamental frequency of the drop of water, and it flattens into a disk. Then they modulate it at the first harmonic (octave) of this pitch and it becomes elongated, like a sausage. This sausage, however, is oscillating. The ends move together and the sides move apart, forming new ends so that it was like a “plus symbol” but with only one line visible at a time, at the peak of each oscillation. When they modulate the frequency at the third harmonic the water forms a triangle, also oscillating with another one so that both together would be a Star of David, but only one was fully formed at a time.
And so they go on. Each harmonic’s shape has the same amount of sides as its sequence number; 1 = circle, 2 = sausage, 3 = triangle, 4 = square, 5 = pentagon and so on. Obviously cymatics made using metal plates and other objects are just showing you complex versions of these basic shapes, made so by the extra factors being brought in by the objects’ physical properties.
And so, the harmonic series can be directly linked to geometry.
Harmonic series music
Here is some music that was made using a VST synthesizer called "Omnisphere 2". It can have each individual note adjusted to exact Hz frequencies and so can play any scale that you like. In this music it has been re-tuned to play only notes from the harmonic series.
The voice sounds are real human voices with nice natural harmonics, you can hear these harmonics ringing like bells and playing "ghost" melodies that are perfectly in tune with the actual chords and melodies. Having the intervals between the notes exactly the same as the intervals between the overtones inside each note really works. Tuning music like this creates fractal harmonies that seem to have a very calming and balancing effect on people. While this does work with normal equal temperament tuning, it is not nearly as accurate or as powerful as with proper harmonic tuning.
The voice sounds are real human voices with nice natural harmonics, you can hear these harmonics ringing like bells and playing "ghost" melodies that are perfectly in tune with the actual chords and melodies. Having the intervals between the notes exactly the same as the intervals between the overtones inside each note really works. Tuning music like this creates fractal harmonies that seem to have a very calming and balancing effect on people. While this does work with normal equal temperament tuning, it is not nearly as accurate or as powerful as with proper harmonic tuning.
Just intonation Music
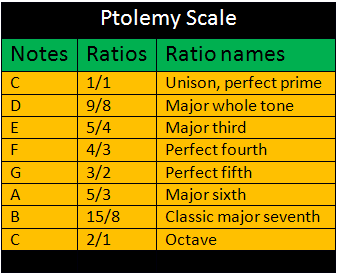
Another type of scale made from the harmonic series is called a "just intonation" scale, just intonation scales are made using ratios. These ratios represent the spaces found between harmonics in the harmonic series. For example the 9/8 whole tone (see image below) is found between harmonics 8 and 9, while the 5/4 major third is found between harmonics 4 and 5.
Ratios with small numbers tend to sound better than ones with larger numbers. This is why the sweetest just intonation scales are made with smallest possible ratios. This is so because small ratios represent spaces between harmonics that are closer to the fundamental of the harmonic series.
Here is some music made using the above just intonation scale. You may notice that it sounds smoother, but not that different to normal equal temperament tuning. This is because equal temperament was based on this, it was the best approximation of this scale possible with equal divisions of an octave. This scale actually is called a "5 limit just intonation" scale because all of its ratios contain only regular numbers with prime factors no higher than 5.
Get books and music here.