Theory of Unity
The ancient stories of unity between mathematics, sound and geometry appear to be true. Somehow the mathematical properties of numbers, the way they sound as audio, and the way they fit together in 3 dimensions mirror each other far more than you would expect. On this page I have summarized everything I have discovered and added links to other pages on this site with more details.
Mathematics
5-smooth numbers are numbers that don't have prime factors larger than 5. Here is a list of the first few 5-smooth numbers: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 64, 72, 75, 80, 81, 90, 96, 100, 108, 120, 125, 128, 135, 144, 150, 160, 162, 180, 192, 200, 216, 225, 240, 243, 250, 256, 270, 288, 300, 320, 324, 360.
In certain forms of mathematics, using 5-smooth numbers helps to keep things whole without too many irrational numbers appearing. This is partly why the Babylonians, the Maya, ancient Hindus and various ancient cultures had a preference for using 5-smooth numbers in some mathematics. Basically 5-smooth numbers have certain type of mathematical usefulness that numbers with higher prime factors don't have.
Music
In music, 5-limit music scales have ratios that contain only 5-smooth numbers. The modern day equal temperament scale is based on and sounds almost exactly the same as a 5-limit scale. To most normal people 5-limit intervals sound smoother and more pleasing to the ear than 7 or higher limit intervals do. Near the bottom of this page you can hear and compare 5 and higher prime limit intervals.
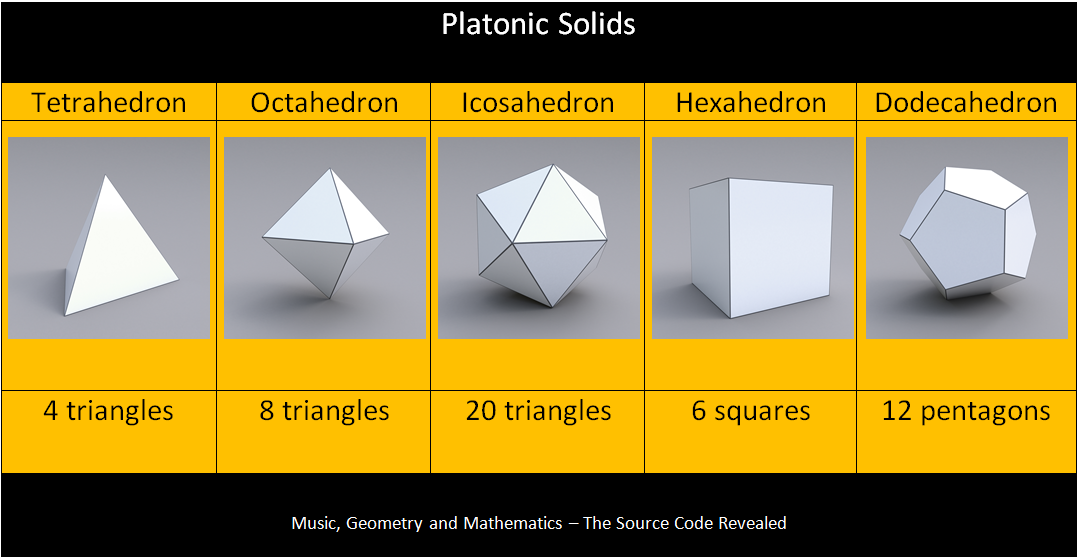
Geometry
In 3 dimensional geometry, the most symmetrical objects are the Platonic and Archimedean solids. These are the basis for many of the strongest and most useful things in our world. They are made by dividing a sphere as evenly as possible using regular polygons. If you count the amounts of sides in the polygons used to make them, and also the amounts of these polygons used, they are always 5-smooth numbers. Prime numbers higher than 5 simply do not work in symmetrical 3 dimensional construction.
Conclusion:
5-smooth numbers simplify mathematics, sound good as music intervals, and also fit together well in 3 dimensions. Next page.